Overview
Big O help us find out how well the problem is solved.
We use it to distinguish that code from good code, good code from great code.
->great developer
What is good code?
1. Readable
2. Scalable
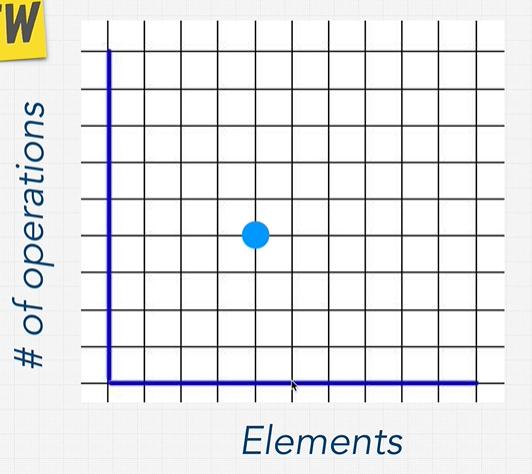
Big O allow us to measure the idea of scalable code.
How can we make sure that there is a way for us to measure in terms of efficiency, what is good code,
what is bad code, and what is code that can scale that as the number of arrays or inputs increases,
it doesn't constantly slow down more and more.
We can compare it to different algorithms or in this case, function using big O and say which one is better than the other when it comes to scale. Regardless of our computer differences.
When we talk about Big O and scalability of code, we simply mean when we grow bigger and bigger with inputs, how much does the algorithm or functions slow down.
When the Elements increase, the number of operations increased over and over. Some increase much, some doesn't increase much.
Instead of using performance and using time to measure the efficiency of our function, we can just calculate how many operations a computer has to perform because each operation takes time on a computer.
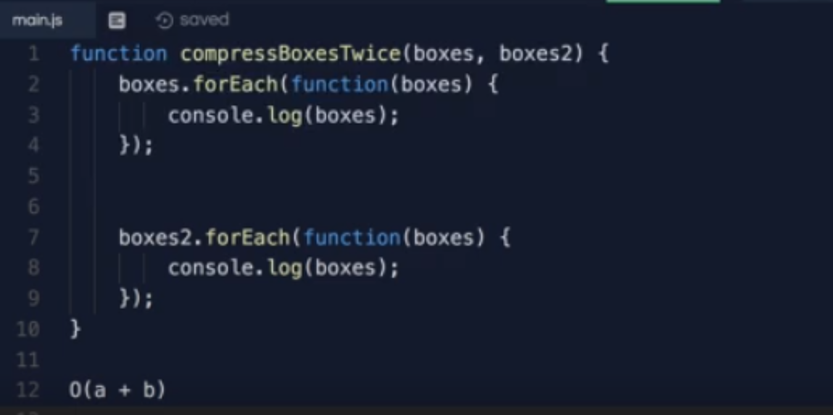
O(n)
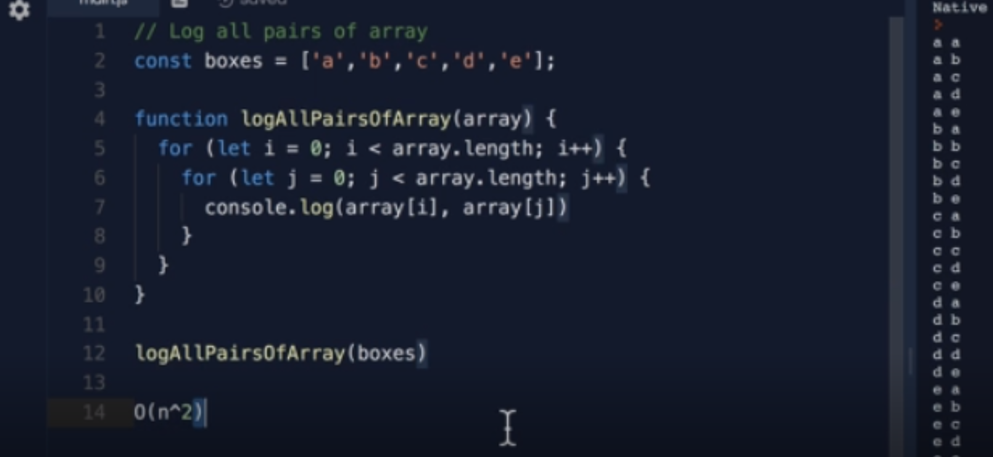
The picture describes that 4 item in an array.
We do the asking loop "is it the nemo ?" 4 times 4 operations
As the items increased, the operation increased.
This is linear. We can say this findNemo notation O(n).
As the item increased, we find the time scaled.
O(1)
This is O(1), what we called constant time.
It is how many items in boxes, we just grasping the first item in the array.
The number of operations just stay flat.